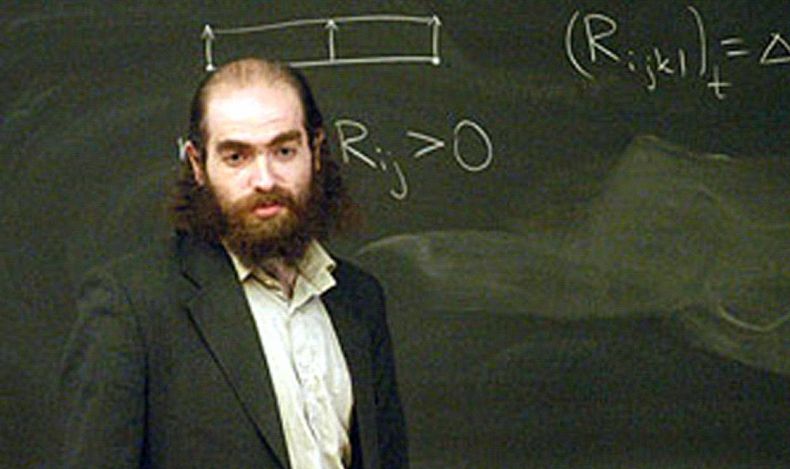Ce duel entre le gardien du temple et le génie effronté montre la violence des mathématiques.
« Lorsque le sens est trop plein pour que le mythe puisse l’envahir, il le tourne, le ravit dans son entier. C’est ce qui arrive au langage mathématique. En soi, c’est un langage indéformable, qui a pris toutes les précautions possibles contre l’interprétation : aucune signification parasite ne peut s’insinuer en lui. Et c’est pourquoi précisément le mythe va l’emporter en bloc : il prendra telle formule mathématique (E = mc²), et fera de ce sens inaltérable le signifiant pur de la mathématicité. On le voit, ce que le mythe vole ici, c’est une résistance, une pureté. Le mythe peut tout atteindre, tout corrompre, et jusqu’au mouvement même qui se refuse à lui en sorte que plus le langage-objet résiste au début, plus sa prostitution finale est grande : qui résiste totalement, cède ici totalement : Einstein d’un côté, Paris Match de l’autre. On peut donner de ce conflit une image temporelle : le langage mathématique est un langage achevé, et qui tire sa perfection même de cette mort consentie ; le mythe est au contraire un langage qui ne veut pas mourir : il arrache aux sens dont il s’alimente une survie insidieuse, dégradée, il provoque en eux un sursis artificiel dans lequel il s’installe à l’aise, il en fait des cadavres parlants. » .
Ce que Roland Barthes disait du mythe Einstein n’a pas perdu de sa pertinence depuis lors, bien au contraire. En 2006, le mythe sut une nouvelle fois prostituer le sens mathématique – cette-fois ci de la résolution par Grigori Perelman de la conjecture de Poincaré.
C’est ce vol de sens que Philippe Zaouati restitue dans son troisième roman, dont la prose élégante fait preuve d’une finesse psychologique et d’une courtoise clarté : même aux néophytes, la conjecture de Poincaré comme les autres problèmes mentionnés sont savamment vulgarisés – il faut y voir l’expérience d’un auteur de deux essais de finance. Le récit rend hommage à la Russie de deux façons : d’une part, par l’opposition dialectique des points de vue divergents des deux protagonistes, méthode chère à Dostoïevski que Perelman, bien malgré lui, n’est pas sans rappeler ; d’autre part, par les heureuses descriptions de Saint-Pétersbourg, qui ne saurait être réduite à un décor facultatif, mais tient lieu de personnage à part entière.
Un silence lourd de sens
En apparence, l’intrigue est simple : le flegmatique John Ball, président de l'Union mathématique internationale, doit convaincre Perelman, récipiendaire de la médaille Fields, d’assister à la cérémonie (22 août 2006). Pour faire revenir à la raison cet « homme qui menace la paix de la discrète communauté » et « réso[udre] l’équation Perelman » . Il part pour Saint-Pétersbourg, deux jours durant (11 et 12 juin 2006). Va se jouer une épreuve de force entre les deux adversaires : pour ce combat, pas d’armes, pas de violence physique, seules les inépuisables et subtiles ressources de l’intelligence, mâtinées de rhétorique et d’informations biographiques, contenues dans « un gros cartable en cuir noir usé et distendu » . Le verbe suffira-t-il de levier archimédien pour changer la décision de Perelman ? De suspense, sur ce point, il n’y a pas : comme le précise l’auteur dans une brève notule, l’auteur se fonde sur des éléments biographiques authentiques (à savoir, la rencontre entre Ball et Perelman, le refus définitif de ce dernier) pour imaginer ce que Ball n’a pas dévoilé (« Il y a des choses confidentielles, des échanges qui resteront entre lui et moi » , dit-il à l’auteur), ce que le titre indique : la teneur de ces « refus ». Ce n’est donc pas une joute chevaleresque que réserve le duel, mais une longue et minutieuse partie d’échecs entre deux esprits retors, dans laquelle le présent d’énonciation nous plonge, spectateurs de coups de maître.
Bien loin de brider l’imagination du romancier, la contrainte de véracité ici se veut l’écrin de la liberté artiste, la résistance de l’air sans laquelle l’envol de la plume ne pourrait être : « les personnages principaux sont certes inspirés de Grigori Perelman et de John Ball, mais les mots que j’ai mis dans leur bouche traduisent la plupart du temps mes propres questionnements. » De la même façon, loin d’un simple et bête conflit entre deux fortes têtes, d’un antagonisme purement négatif, les interlocuteurs cherchent, non pas à avoir raison de l’autre, mais avec l’autre ; non pas à se contredire, mais à se réfuter. Autrui s’oppose comme l’ami permet au je de surmonter le moi. Telle est l’exigence de l’amitié chez Nietzsche : « Si l’on veut avoir un ami il faut aussi vouloir faire la guerre pour lui : et pour la guerre, il faut pouvoir être ennemi. Il faut honorer l’ennemi dans l’ami. Peux-tu t’approcher de ton ami, sans passer à son bord ? En son ami on doit voir son meilleur ennemi. C’est quand tu luttes contre lui que tu dois être le plus près de son cœur. » . Contre, tout contre Perelman, Ball le sera, à mesure de ses échanges, et d’un éprouvant exercice de télépathie – télépsychie serait plus à propos, tant l’ouvrage évite très justement l’écueil du pathos. Si cette séance de spiritisme voisine les lisières de l’occultisme, c’est surtout la profonde empathie de Ball pour la réserve de Perelman qu’il faut retenir, comme la déconstruction de l’image d’Epinal que l’on peut volontiers avoir du génie russe.
L’ermite des mathématiques
A quoi tient le mythe Perelman ? D’une part, au prestige de la science mathématique, formelle et pure, mais aussi à ses devanciers, qui prétendaient encore à la polymathie et, partant, à une vision synoptique du réel. Perelman a résolu la conjecture de « l’un des derniers chercheurs généralistes, capable de passer d’un problème de géométrie à des équations d’astronomie ou de dynamique des fluides, capable de disserter sur la forme de l’univers en mêlant mathématiques et philosophie. (…) Aujourd'hui, même les génies sont condamnés à se focaliser sur des têtes d’épingle » . D’autre part, la figure médiatique d’un autiste non-humain, sinon inhumain, d’un Prométhée violant les mystères divins du monde, au physique de prophète de l’Ancien Testament : « une apparence de savant fou, une barbe mal taillée, des cheveux longs, d’épais sourcils, un regard étonnamment clair, presque inquiétant, des vêtements disparates et usés… » .
Certes, Perelman fascine, mais son refus n’est-il pas convenu ? Jankélévitch avait déjà prévenu : « de tous les conformismes, le conformisme du non-conformisme est le plus hypocrite et le plus répandu aujourd’hui ». Le plus haut degré du snobisme consiste à dédaigner les prix, et Perelman ne pourra empêcher d’être récupéré par le vulgaire révolutionnaire, qui verra en lui le parangon de la subversion, certifié antisystème. A quoi bon se taire, ne pas jouer le jeu, se sacrifier à l’idée qu’on veut (se) donner de soi, puisque les commentateurs profiteront du silence du Russe pour donner à son geste des motifs idiots, ou vulgaires. Camus parlait d’or : « les martyrs doivent choisir d’être oubliés, raillés ou utilisés. Quant à être compris, jamais. » . C’est ce redoutable argument que Ball mettra en avant : « Certains ont pu prendre cette indifférence pour du mépris. » « Vous deviendrez le héros des humbles ou plus probablement celui des révolutionnaires de pacotille » ; et que Perelman, tant bien que mal, récusera.
John Ball, comme en son temps Blaise Pascal, aura sa nuit : il ne verra pas Dieu, mais en un homme divin sous certains aspects, et défera la pelote de sa personne. Loin d’offrir une lecture simple, la vie de Perelman est un palimpseste où les origines juives, la morgue américaine, l’amour filial et les années soviétiques finissent par s’emmêler. Ball prendra conscience, au gré de ce jeu de glaces bien étudié, de l’importance des « petites contingences indignes de la pureté de la discipline » : « les bavardages, les on-dit, les mesquineries de mathématiciens sans talent, la jalousie des médiocres, l’arrogance des aigles ». A tel point que Ball en viendra à se demander si, à travers le procès qu’il dresse à Perelman, il ne fait pas du même coup celui de son temps. Le roman bat en brèche l’image d’un Perelman brut et buté : il « fait preuve d’une grande érudition, d’une capacité à rendre proches des sujets apparemment sans lien, dans une vraie profondeur culturelle, et pourtant, même s’il parvient par moments à embrasser le monde entier dans sa pensée, il revient irrémédiablement à ses obsessions, à cette quête sans fins des moindres imperfections. Il aborde les œuvres d’art comme les jeux, l’Histoire comme le temps qu’il fait. Il fabrique des systèmes. » . C’est sans doute à cet absolu, la neutralité de l’abstraction, que ce brillant esprit prétend : sa vie se doit dès lors de se déprendre des petites préoccupations de la quotidienneté, d’oublier sa petite personne et de se vouer, corps et âme, à la beauté formelle, au silence qui lui est propre